蕾师师 发自 凹非寺

量子位 报道 | 公众号 QbitAI

数学和计算机的关系，一直是 你中有我、我中有你。

计算机程序离不开数学，同时也给数学计算带来便利。

国外知名科普网站Quanta Magazine，对2020年计算机、数学这两门学科的几项重大突破，进行了盘点。

这里面，有困扰了，也有AI与数学结合的身影。

当然，两名数学家疫情隔离期间，破解陶哲轩挑战失败的，也榜上有名。

一起来看看。

TOP1：“量子纠缠”重大突破

今年，计算机领域最重要的突破，是MIP*=RE的证明。

它的证明，意味着利用量子逻辑来计算的量子计算机 （而非利用0和1进行计算的经典计算机），可以从理论上验证大量问题的答案。

来自悉尼科技大学、加州理工学院、德克萨斯大学奥斯汀分校、和多伦多大学的五位计算机科学家，将研究成果联名发表在了一篇叫做《 MIP * = RE》的论文上。

这篇论文证明，由经典验证与多个量子理论验证相互作用而确定的语言类别MIP，等同于递归可枚举语言类RE。

也就是说，MIP*=RE多方交互式证明、加上量子纠缠的计算能力，给 图灵停机问题提供了一个思路。

对于这篇论文的结论，物理学家在里面看到Tsirelson的物理问题的答案，数学家在里面得到了Connes嵌入猜想的答案。

作者之一的Henry Yuen说道：“如同 盲人摸象一样，不同科学领域的人，领略到不同部分，虽然都是正确的，但是都还没搞清楚大象的原貌。”

80年代，计算机科学家发明了交互证明理论和概率可验证明 (PCP)，MIP* = RE则是经典的PCP定理，能够在量子纠缠的帮助下递归到无穷。

论文得出结论说，两台机器相互纠缠、相互验证，可以用于解决图灵停机问题。同时，还证明了 Connes嵌入猜想是错误的。

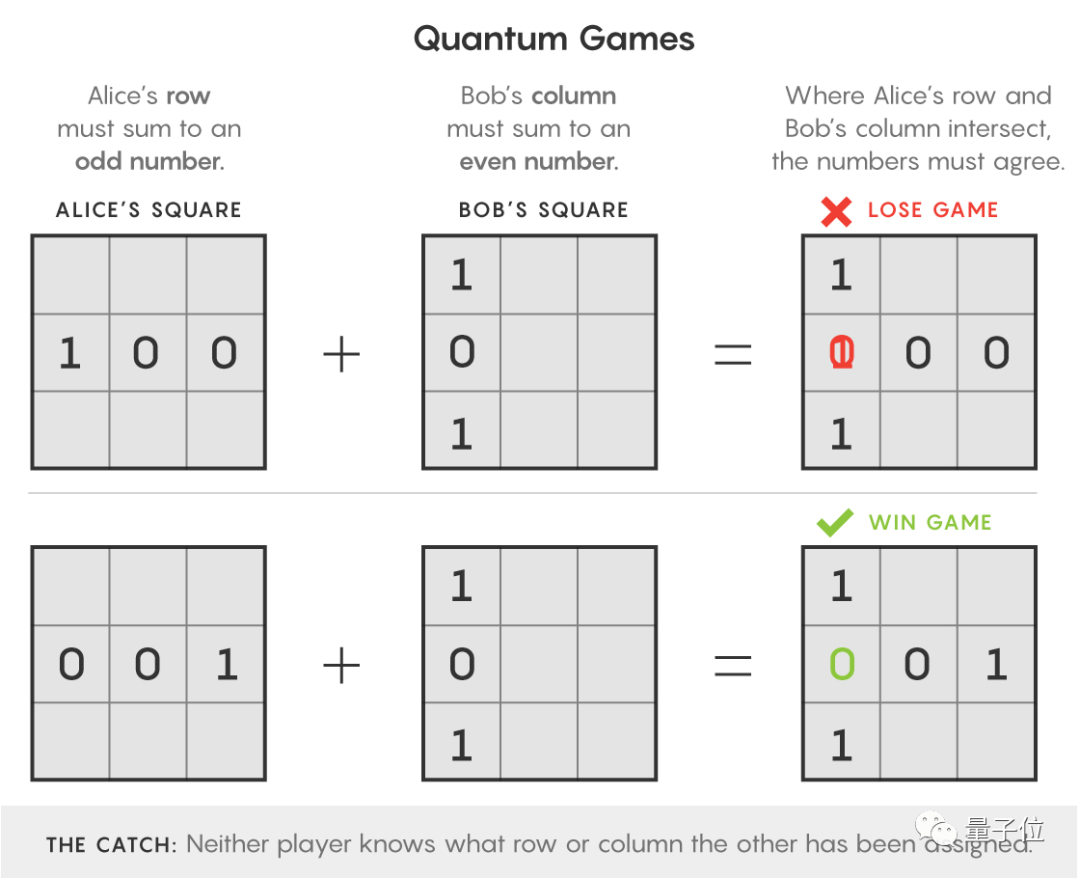
他们还引用了经典的两个博弈互证游戏Bell / CHSH，两者无穷无尽的纠缠验证，会提高游戏的胜率。所以最终问题，还是怎么让这个纠缠验证的过程停止的问题。

此外，这篇论文的一作，是悉尼科技大学量子软件与信息中心季铮锋教授。

季铮锋曾于2007年，获得清华大学计算机科学与技术的博士学位。

论文地址：

https://arxiv.org/abs/2001.04383

TOP2：破解“康威扭结”

今年6月，英国著名数学家约翰·康威（John Conway）因患新冠肺炎逝世，留下一个困扰数学界 50年的难题“康威扭结”（Conway Knot）。

在他逝世一个月之后，德州大学奥斯汀分校的一位博士小姐姐Lisa Piccirillo，花了 一周的时间将其解决了。

多年来，数学家们发现了形形色色的扭结，这些结在拓扑学上可切，但并不是平滑可切。然而，这些扭结的交叉都大于12。

而在交叉点数小于12的扭结中，只有康威结的切片状态一直无法找到。

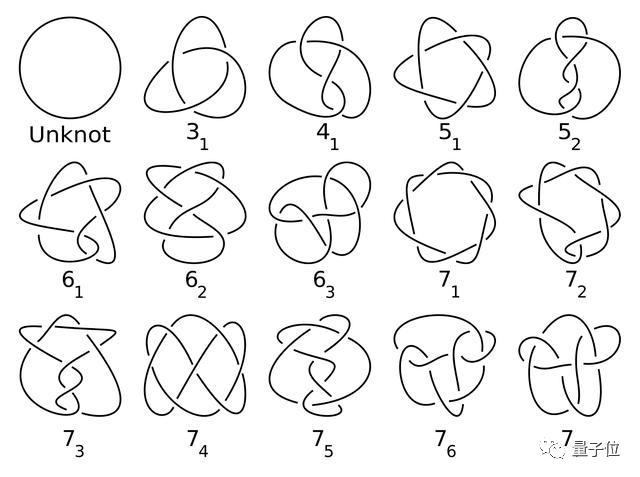
康威扭结是否平滑可切为何如此重要？

因为 平滑可切的扭结，为数学家提供了一条探索四维空间奇特属性的途径。

所以，康威扭结是否为平滑可切，成为了扭结理论重大突破的硬性标准。

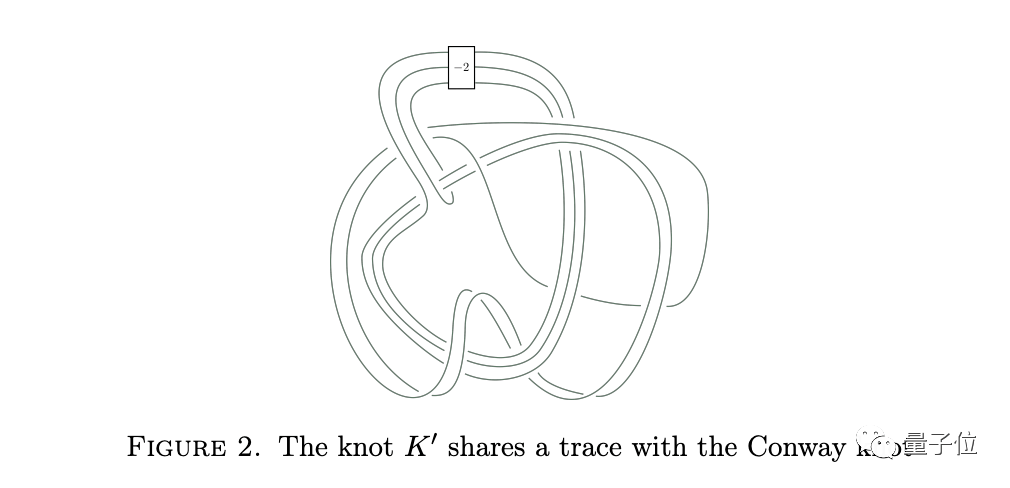
Lisa认为，如果可以为康威扭结构造一个相同迹的扭结，那么也许可以更好地与可切不变性配合使用。

于是，她设法构造了一个复杂的扭结，它的迹与康威扭结相同。Lisa使用了一种叫做拉斯穆森S不变量（Rasmussen’s s-invariant）的工具。

结果显示她构造出来的扭结不是平滑可切的，因此推断出， 康威扭结也不是平滑可切的。

“这是一个非常美丽的证明。”数学家们纷纷赞叹说。

阅读延伸：

https://mp.weixin.qq.com/s/4wGmSxKGFVEqW_wdWWVtog

TOP3：参加IMO的AI

数学已经有了数千年的发展历史，而人类的记忆力有限，即使是一流的数学家，也记不住全部的数学公式和定理。

于是很多数学科学家转向了“ 数学数字化”，将数千年累积的数学成果，建成一个数字图书馆。